A todo docente le llega, más tarde o más temprano, la pregunta que siempre es complicado responder: ¿Para qué me sirve esto?
Y a pesar de existir varias respuestas a esa pregunta, muy interesantes, por cierto, a veces las matemáticas se debe aprender solo porque se trata de la herramienta más poderosa para modelizar la realidad en muchos y variados aspectos. Por eso es tan importante aprender matemáticas y si necesitas ayuda, recurrir a un profesor particular de matemáticas.
Pero un tema que tiene una respuesta simple es cuando el cuestionamiento se hace sobre la ecuación cuadrática. Es una operación tan simple que sorprende a algunos enterarse de que lo estará usando hasta en ejercicios de integrales triples, o diagonalizando matrices.
La ecuación cuadrática ha sido motivo de grandes disputas a lo largo de la historia de las matemáticas, que han permitido desarrollar lo que hoy conocemos como “fórmula resolvente de una ecuación cuadrática”.
Para empezar, hay que identificar qué es una ecuación cuadrática, es decir, poder diferenciar una ecuación cuadrática de otra que no lo es. Veamos entonces:
Una ecuación cuadrática se trata de la igualdad entre un polinomio de grado 2 y el número 0. El grado de un polinomio es el mayor exponente con que aparece la variable. Entonces, si es de grado 2, aparecerá una X elevada al cuadrado. Y ese será el mayor exponente, por lo tanto, solo puede aparecer elevada a 1 y a 0. Quedaría así:
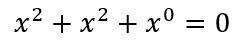
Además, cada término puede aparecer multiplicado por algún número, llamado coeficiente. Si a esos números los llamamos a, b y c, quedará así:
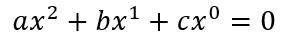
Y finalmente, teniendo en cuenta que elevar algo a 1 es lo mismo que no elevarlo y elevar a cero, da 1, queda:
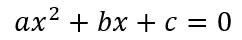
Una vez identificada la ecuación, y viendo que cumple los requisitos para ser una ecuación cuadrática, resolveremos la ecuación usando la siguiente fórmula:
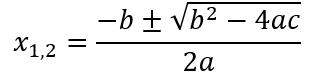
Por ejemplo:
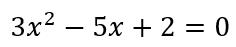
Tendremos:
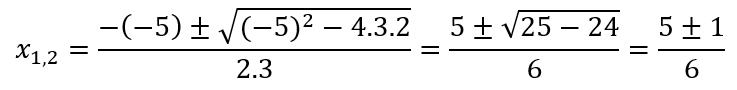
Y finalmente, sumando obtenemos un resultado y restando el otro:
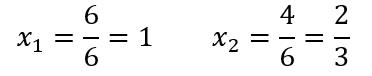
Un caso particular se da cuando el coeficiente del término cuadrático es uno, o sea, cuando a=1.
En ese caso, la ecuación es:
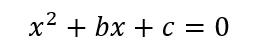
Y se da la propiedad de que:
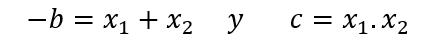
En otras palabras, la suma de las raíces es igual al opuesto de b; el producto de las raíces es igual a c. ¿Cómo ayuda esto a resolver una ecuación cuadrática?
Supongamos la siguiente ecuación:
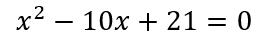
Buscamos, entonces, dos números que sumados den 10 y multiplicados, den 21. Con un poco de práctica, es directo ver que se trata de 3 y 7. En efecto, 3+7=10 y 3.7=21.
Consejos finales:
- Siempre realizar los pasos necesarios para que todos los términos queden de un lado y del otro quede solamente un cero.
- Tener cuidado con los signos de cada número al remplazar en la fórmula.
- Si dentro de la raíz queda cero, entonces se trata de una cuadrática con una sola solución, de la que se dice que es “doble”.
- Si dentro de la raíz queda un número negativo, entonces la ecuación cuadrática no tiene solución.
(al menos, vale aclarar, dentro del conjunto de los números reales, pero las soluciones complejas son para otro artículo).



