La derivación y la integración son dos conceptos clave del cálculo, una disciplina fundamental de las matemáticas que estudia los cambios y las áreas bajo las curvas. En este artículo, se presentarán las definiciones, las fórmulas básicas y algunos ejercicios prácticos que ayudarán a los estudiantes a comprender mejor estos conceptos.
Nuestros profesores de matemáticas
Este material complementará las clases y será un recurso valioso tanto para alumnos como para otros profesores que deseen enriquecer sus métodos de enseñanza.
¿Que es una derivación en matemáticas?
La derivación es el proceso de encontrar la tasa de cambio de una función con respecto a una variable. En términos simples, la derivada de una función en un punto específico indica cómo cambia la función cuando la variable independiente varía infinitesimalmente. Matemáticamente, la derivada de una función f(x) respecto a x se denota como f′(x) o df/dx.
Fórmula de la derivada:
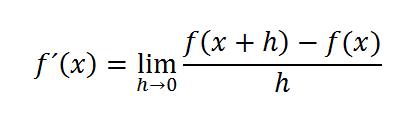
Reglas básicas de derivación
- Derivada de una constante: Si c es una constante, entonces d/dx(c)=0.
- Regla de la potencia: Si f(x)= x^n, entonces f′(x)=nx^{n-1}.
- Regla del producto: Si f(x)=u(x)v(x), entonces f′(x)=u′(x)v(x)+u(x)v′(x).
- Regla del cociente: Si f(x)=u(x)/v(x), entonces f′(x)=u′(x)v(x)−u(x)v′(x)/v(x)^2.
- Regla de la cadena: Si y=f(g(x))y, entonces dy/dx=f′(g(x))⋅g′(x).
Ejemplos de derivación
-
Ejemplo 1: Encuentra la derivada de f(x)= 5x^3.
- Aplicamos la regla de la potencia: f′(x)=5⋅3x^{3-1} =15x^2.
-
Ejemplo 2: Encuentra la derivada de f(x)=sin(x).
- Usamos la derivada conocida: f′(x)=cos(x).
¿Que es una integración?
La integración es el proceso inverso a la derivación. Se utiliza para encontrar la función original a partir de su derivada, o para calcular el área bajo una curva. La integral de una función f(x) se denota como ∫f(x) dx. Existen dos tipos principales de integrales: indefinidas y definidas.
Integral indefinida:
Es la antiderivada de una función y se representa como:
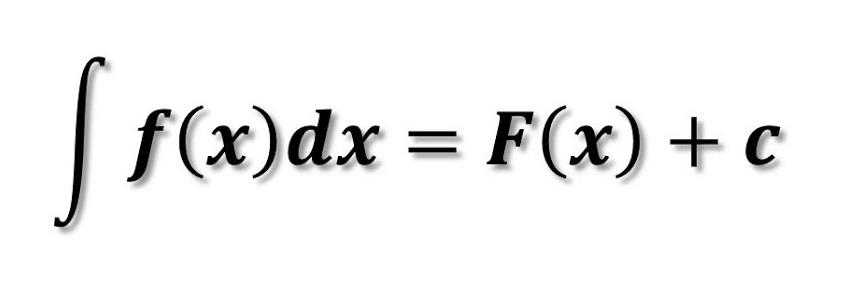
donde F(x) es una función cuya derivada es f(x), y C es una constante de integración.
Integral definida:
Calcula el área bajo la curva de f(x) desde a hasta b:
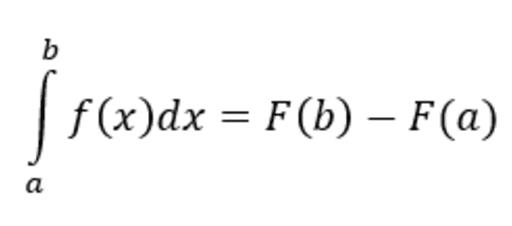
Reglas básicas de integración
- Integral de una constante: ∫cdx=cx+C.
- Regla de la potencia: ∫x^n dx = {x^(n+1)/(n+1)} + C (para n≠−1).
- Integrales de funciones trigonométricas:
- ∫sin(x)dx=−cos(x)+C
- ∫cos(x)dx=sin(x)+C
Ejemplos de integración
-
Ejemplo 1: Encuentra la integral indefinida de f(x)= 7x^2.
- Aplicamos la regla de la potencia: ∫7x^2 dx= 7 ⋅ {x^(2+1)/(2+1)} + C = 7 · {x^3/3} + C = 7/3 x^3 + C.
-
Ejemplo 2: Encuentra la integral definida de f(x)=2x desde 0 hasta 2.
- Primero, encontramos la integral indefinida: ∫2x dx = x^2+C.
- Luego, evaluamos de 0 a 2: [x2]^2/0 = 2^2 - 0^2 = 4.
Comprende las derivadas y las integraciones
Comprender la derivación y la integración es crucial para los estudiantes de matemáticas, ya que estos conceptos son la base de muchas aplicaciones en física, ingeniería y otras ciencias. Como docentes, es nuestro deber ofrecer recursos adicionales y apoyo a nuestros alumnos, y esperamos que este material os resulte de gran utilidad.
Recuerda que la práctica continua y la resolución de ejercicios adicionales son esenciales para dominar estos conceptos. ¡Buena suerte y sigue explorando el fascinante mundo del cálculo!





