INTRODUCCIÓN
Es muy común que tras estudiar un tema concreto de matemáticas, el alumno sepa resolver los ejercicios que se le proponen, pero que le cueste mucho resolver problemas planteados de forma natural.
Por ejemplo, si el tema era la resolución de sistemas de dos ecuaciones con dos incógnitas, el alumno sabrá responder a algo como Resolver el siguiente sistema: x + y = 100 ; x – ¼· y = 70
Clases particulares de matemáticas
Pero le suele costar mucho más resolver un problema de enunciado como:
En un examen tipo test, las preguntas correctas suman un punto y las incorrectas restan ¼ de punto. En total hay 100 preguntas y no se admiten respuestas en blanco. Un alumno ha obtenido una nota de 7 sobre 10. Calcular el número de preguntas que contestó correctamente y las que contestó incorrectamente.
El procedimiento recomendado se resume en el siguiente gráfico y consta de 4 pasos.
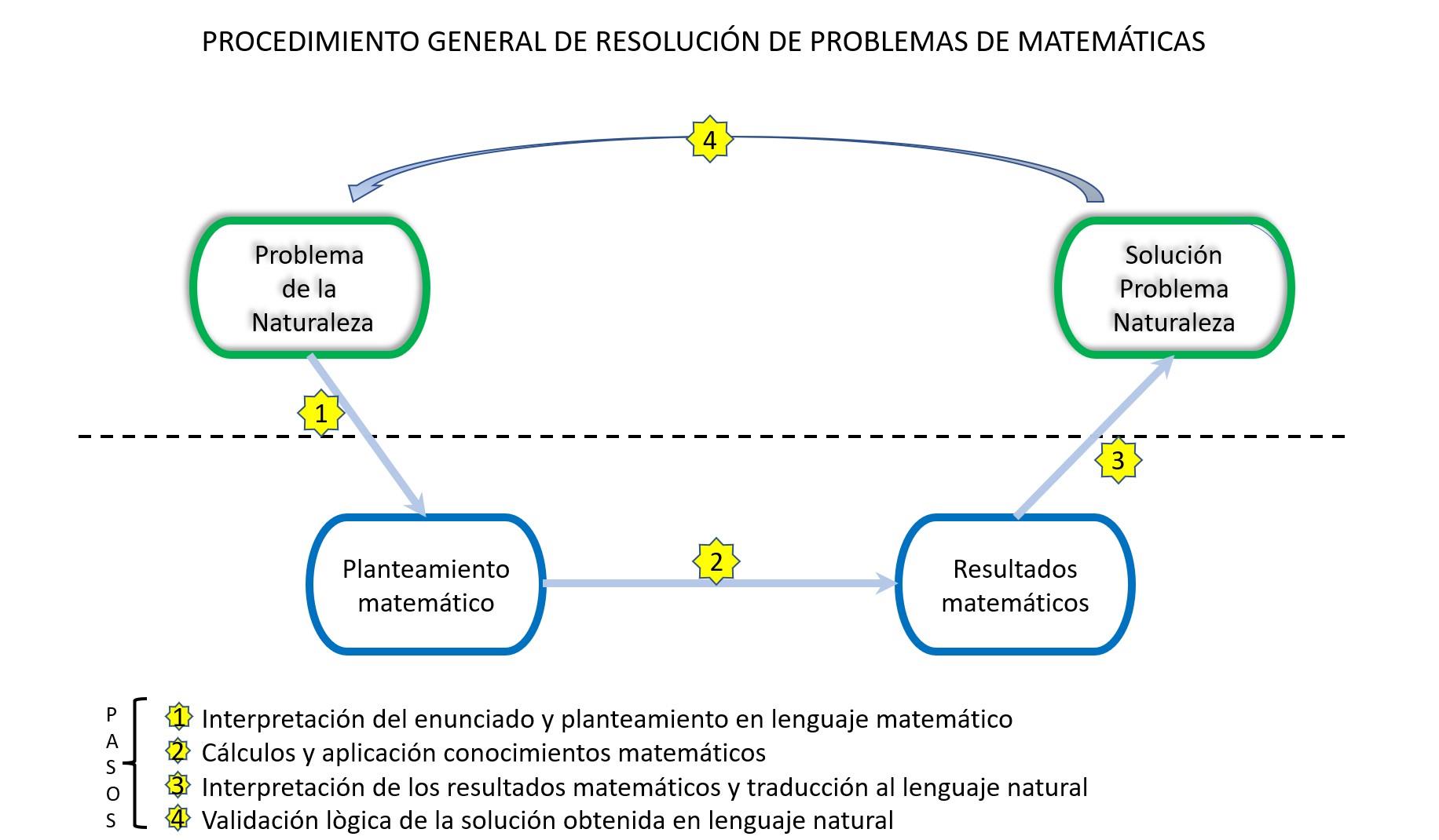
PROCEDIMIENTO
PASO 1
En primer lugar, debemos “traducir” el lenguaje natural del enunciado (que corresponde a un problema “real” de la naturaleza) al lenguaje matemático.
En el ejemplo sería plantear lo siguiente:
Sea x el número de respuestas correctas e y el número de respuestas incorrectas.
Sabemos que x + y = 100 (que es el total de respuestas a contestar)
También sabemos que 1· x – ¼· y = 70 dado que suma 1 punto por cada x, resta ¼ de punto por cada y, y además la nota del alumno debemos pasarla a base 100 (nos dan un 7 sobre 10, pero tenemos que considerarla sobre 100 preguntas, esto es, 70 sobre 100).
Por tanto, tenemos que resolver el siguiente sistema:
x + y = 100
x – ¼· y = 70
PASO 2
Para la resolución del problema ahora ya planteado en lenguaje matemático, aplicamos los conocimientos matemáticos adquiridos de cálculos, fórmulas, teoremas, etc. para ese tema concreto.
En el ejemplo, aplicaremos los conocimientos sobre cómo resolver un sistema de dos ecuaciones con dos incógnitas, por ejemplo, por substitución:
x + y = 100 à x = 100 – y
x – ¼· y = 70 à 100 – y – ¼·y = 70 à -y – 1/4y = 70 – 100 à -5/4·y = – 30 à y = (4/5)·30 = 24
Luego x = 100 – y = 100 – 24 = 76
Resultado matemático: x = 76 ; y = 24
PASO 3
Una vez obtenidos los resultados matemáticos gracias al paso anterior, realizamos la correspondiente traducción al lenguaje natural.
En el ejemplo, diremos que
el alumno ha respondido correctamente a 76 preguntas e incorrectamente a 24 preguntas
PASO 4
Finalmente, ya en el “mundo natural”, debemos hacer las comprobaciones lógicas que se nos ocurran releyendo el enunciado y viendo si lo que hemos expresado como solución al problema tiene o no sentido.
En el ejemplo, podríamos hacer varias comprobaciones, a destacar:
1. La suma de respuestas correctas e incorrectas tiene que dar el total de preguntas contestadas, esto es 100.
2. Como la nota es un 7, y las respuestas correctas suman 1 punto, debemos tener como mínimo 70 respuestas contestadas correctamente. Si hemos respondido una cifra menor, seguro que nos hemos equivocado.
3. Evidentemente, no podemos dar un número negativo por respuesta (si nos saliera algo así, respuestas correctas = -3, está claro que nos hemos equivocado en la resolución matemática del problema, paso 2).



